TRAZADOS BÁSICOS DE DIBUJO GEOMÉTRICO

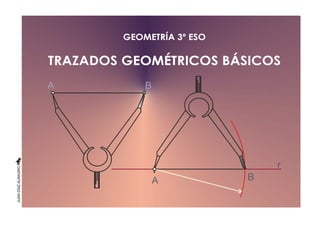
GEOMETRÍA 3º ESO
TRAZADOS GEOMÉTRICOS BÁSICOS
A
A B
B
r

Geometría 3º ESO TRAZADOS GEOMÉTRICOS BÁSICOS
EL PUNTO
Es la Intersección de dos rectas
Se designan con letras mayúsculas o números:
A, B, C...P, Q, R,...1, 2, 3,...
P

LA LÍNEA
Es una sucesión de puntos unidos entre sí. Una línea es un punto en movimiento.
Si va siempre en la misma dirección se trata de una línea recta. Si cambia de dirección,
forma una curva.
Las rectas se designan con letras minúsculas:
r
u
t
s

RECTA
Es una linea cuyos puntos siempre siguen la misma trayectoria y no tiene principio ni final.
Sus extremos se tocan en el infinito.
Las rectas se designan por una letra minúscula
r

LA LÍNEA CURVA
Es una sucesión de puntos que no siguen la misma dirección.
Es la trayectoria de un punto en movimiento
Las curvas se designan con letras minúsculas: a, b, c, ...r, s, t...
r
t
s

SEGMENTO
Es una PARTE DE RECTA LIMITADA EN SUS EXTREMOS POR DOS PUNTOS.
Los segmentos se designan con letras minúsculas: segmento a,
o por dos letras mayúsculas en sus extremos: segmento AB o AB
a
A B

SEMIRRECTA
Es una RECTA LIMITADA EN UNO DE SUS EXTREMOS.
las semirrectas se designan por la mayúscula del punto que las limita
y la minúscula de la recta
O r

ÁNGULO
Es la PORCIÓN DE PLANO COMPRENDIDO ENTRE DOS
SEMIRRECTAS QUE TIENEN EL MISMO ORIGEN.
Las semirrectas son los LADOS del ángulo, y el punto de
intersección el VÉRTICE.
Los ángulos se designan por una letra mayúscula en su vértice
o por letras griegas minúsculas
A
a

PLANO
Es la SUPERFICIE FORMADA POR TRES PUNTOS NO ALINEADOS.
También podemos decir que un plano queda definido por dos rectas que se cortan,
o por dos rectas paralelas, o por una recta y un punto que no le pertenece
a b g

OPERACIONES CON REGLA Y COMPÁS
Transporte de un segmento cualquiera AB
Trazamos una recta r
A B
r

Cogmos la medida del segmento
con el compás
A B
r

Cogemos la medida del segmento
con el compás, y marcamos en la
recta r trazada un punto A
A
A
B
r

Haciendo centro en A, trazamos un arco que corta a la recta r
en el punto B. Así, ya está trasladado el segmento
A
A B
B
r

V
V´
a
Transporte de un ángulo
Trazamos una recta, y sobre ella marcamos el vértice V´.

V
1
2
a
V´
Sobre el ángulo dado, trazamos un arco de medida
arbitraria con centro en el vértice, que cortará los lados del vértice en
los puntos 1 y 2

V
1
2
2´
a
V´
Medimos con el compás el arco 1V2 y lo trazamos sobre V´.
Dicho arco corta a la recta en el punto 2

V
1
2
2´
1´
a
V´
Medimos con el compás la distancia 2-1 y la trasladamos sobre 2´.
Así obtenemos 1´

V
1
2
2´
1´
a
V´
Uniendo V con 1 ya tenemos el ángulo transportado

SUMA DE SEGMENTOS
Hallar la SUMA de los SEGMENTOS AB y CD
A
D
B
C
A B
1. Dibujamos el segmento AB
sobre una recta auxiliar

SUMA DE SEGMENTOS
A
D
B
C
A
D
C
B
2. A continuación, dibujamos
sobre la misma recta el
segmento CD de forma
consecutiva, haciendo
coincidir el extremo C
con el B

SUMA DE SEGMENTOS
A
D
B
C
A
D
C
B
AB + CD
3. El segmento resultante AD
es la suma de AB + CD

DIFERENCIA DE SEGMENTOS
Hallar la DIFERENCIA de los SEGMENTOS AB y CD
A
D
B
C

A
D
B
C
A B
1. Dibujamos el segmento AB
(el más grande)
sobre una recta auxiliar

C D
A B
2. Dibujamos el segmento
CD (el más pequeño)
dentro del AB, haciendolos
coincidir por uno de sus
extremos
D
B
A
C

T2. TRAZADOS FUNDAMENTALES EN EL PLANO. Paralelas, Perpendiculares, Mediatrices
D
B
C
D
C
A B
AB - CD
3. El segmento resultante
será DB, diferencia entre
AB y CD
A

MEDIATRIZ DE UN SEGMENTO
Trazar la MEDIATRIZ m y el PUNTO MEDIO del SEGMENTO AB
A B
MEDIATRIZ de un segmento es la recta perpendicular a él en su punto medio.
Divide al segmento en dos partes iguales, y tiene la propiedad de que todos sus puntos
equidistan de losextremos A y B del segmento.
Por tanto, es un lugar geométrico, ya que todos sus puntos
gozan de la misma propiedad.

1. Trazamos dos arcos iguales,
desde A y desde B, que midan
más de la mitad de dicho
A B
segmento.
Ambos arcos se cortarán en
los puntos 1 y 2

A
1
2
1. Trazamos dos arcos iguales,
desde A y desde B, que midan
más de la mitad de dicho
B
segmento.
Ambos arcos se cortarán en
los puntos 1 y 2

1
m
A B M
2
2. Unimos los puntos 1 y 2,
obteniendo así la
MEDIATRIZ del
segmento AB

Aplicación del trazado de la MEDIATRIZ en la DIVISIÓN DE UN SEGMENTO (números pares)
División de un segmento AB en 2, 4, 8...o cualquier nº par de partes
A B

1. Trazamos la mediatriz
de AB, obteniendo así
el punto medio C y divi-diendo
A C B
AB en dos partes
iguales

2. Trazamos las mediatrices
de AC y CB, obteniendo así
los puntos D y E, y dividiendo
el segmento en 4 partes
A D C E B
iguales
Si continuáramos haciendo
mediatrices obtendríamos
8, 16, 32...partes iguales

T2G. eToRmAeZtAríaD O3ºS E FSUON D A M E N T A L E S T ERNA ZEAL DPOLASN GOE. POaMraÉleTlRasIC, POeSrp BenÁdSicICuOlaSres, Mediatrices
PARALELAS
Las paralelas son rectas coplanarias
que no tienen ningún punto en común,
es decir, se cortan en el infinito

TRAZADO DE PARALELAS CON ESCUADRA Y CARTABÓN
Tenemos la recta r y queremos hacer rectas paralelas por encima y por debajo. Sigue los pasos que a continuación se indican:
r r r r
1. Situamos la escuadra, por su lado
más largo, justo sobre
el segmento
2. Colocamos el cartabón pegado
a uno de los otros dos
lados de la escuadra
3. Sujetamos muy fuerte el cartabón
y deslizamos suavemente la escuadra
sobre él hacia arriba o hacia abajo
para hacer las paralelas
correspondientes
PARALELAS

Trazar una PARALELA a la recta r separada de ella 42 mm
r
PARALELAS

r
1. Para trazar una paralela
a una DISTANCIA deter-minada,
tenemos que
trazar en primer lugar
una perpendicular a
la recta
PARALELAS

r
42 mm
2. Una vez trazada la
perpendicular, medimos
sobre ella la distancia
requerida
PARALELAS

s
r
42 mm
3.Posteriormente trazamos
la paralela, con escuadra
y cartabón
PARALELAS

r
Trazar una PARALELA a la recta r que pase por el PUNTO A
A
PARALELAS

r
1
A
1. Trazamos un arco con
centro en A que corte
a r en el punto 1
PARALELAS

r
A
2 1
2. Con el mismo radio que
el arco anterior, trazamos
un arco con centro en 1 y
radio 1A, que cortará a r
en el punto 2
PARALELAS

r
A 3
2 1
2A
3. Con radio 2A, trazamos
un arco con centro en 1,
que corta al primer arco
trazado en el punto 3
PARALELAS

r
2 1
3
2A
A
4. Uniendo A con el punto 3
obtenemos la paralela
buscada
PARALELAS

PERPENDICULARES
Son perpendiculares entre sí aquellas rectas que al cortarse dividen el plano en
cuatro ángulos rectos (cuatro ángulos de 90º)
d
a e
b
90º
90º
90º
90º 90º
90º
90º
90º

PERPENDICULARES
Trazado de perpendiculares con ESCUADRA Y CARTABÓN
Tenemos la recta r y queremos hacer rectas perpendiculares a la misma. Sigue los pasos que a continuación se indican.
Observa que los dos primeros pasos son iguales a los que realizamos cuando trazamos paralelas:
r r r r
1. Situamos la escuadra, por su lado
más largo, justo sobre
el segmento
2. Colocamos el cartabón pegado
a uno de los otros dos
lados de la escuadra
3. Sin mover el cartabón, giramos la
escuadra sobre su ángulo recto.
Deslizándola en esta posición sobre el
cartabón, podemos hacer tantas
perpendiculares como queramos

Aplicación del trazado de la MEDIATRIZ en EL TRAZADO DE PERPENDICULARES
Trazar la RECTA PERPENDICULAR a la recta r por el PUNTO A, exterior a la recta.
A
r
Hallar la DISTANCIA que hay del punto A a la recta

A
r
1 2
vértice en A que corta a
la recta r en los puntos
1 y 2

A
r
1 2
2. Con centro en 1 y en 2,
trazamos arcos iguales
que se cortarán en el
punto 3.

A
r
1
3
2
trazamos arcos iguales
punto 3.

A
r
1
3
2
3. Si unimos A con el
punto 3 obtenemos la
perpendicular a r por
el punto A

A
r P
1
3
2
4. La distancia de A a la
recta estará en la
perpendicular, ya que la
distancia de un punto a una
recta siempre hay que
tomarla en perpendicular

Trazar la RECTA PERPENDICULAR a la recta r por el PUNTO A, perteneciente a ella
r A

r A
1 2
vértice en A que corta a
la recta r en los puntos
1 y 2

3
r A
1 2
trazamos dos arcos iguales
punto 3.
4

s
3
r A
1 2
3. Si unimos A con
el punto 3 o el 4 obtenemos
la perpendicular a la
recta r
4

Levantar dos PERPENDICULARES al segmento AB por sus extremos,
utilizando dos métodos diferentes (con compás)
A B

A 1 B
1. Con centro en A, trazamos
un arco que corta al
segmento AB en el punto 1

2
A 1
B
2. Con la misma distancia
que el arco anterior
trazamos un arco 1A, que
cortará al anterior en el
punto 2

4
3 2
A 1
B
3. Con centro en 2 trazamos
el arco 2A, obteniendo así
el punto 3. Del 3 al 2
trazamos otro arco que
corta al anterior en el
punto 4

4
3 2
A 1
B
4. Uniendo el 4 con A
obtenemos una
perpendicular al
segmento AB desde
el punto A

4
3 2 O
A 1 5
B
5. Para la segunda
perpendicular, trazamos
desde B un arco cualquiera
que corta al segmento AB
en el punto 5. Desde el 5
trazamos el arco 5B,
obteniendo así el punto O

4
3 2 O
A 1 5
B
6. Con centro en O,
trazamos la circunferencia
de radio O5 (= OB).

4
A 1 5
6
3 2 O
B
7. Trazamos una recta
del 5 al centro O, que en
su prolongación cortará
a la circunferencia en
el punto 6

4
A 1 5
6
3 2 O
B
8. Uniendo el punto 6
con B, obtenemos
la perpendicular que
buscamos

DIVISIÓN DE UN SEGMENTO EN PARTES IGUALES. TEOREMA DE THALES
Divide el segmento AB en tres partes iguales
mediante el TEOREMA DE THALES
A B

A B
1. A partir de uno de los
extremos del segmento
trazamos una recta auxiliar
en una dirección arbitraria.

A
1
2
3
B
2. Sobre dicha recta
hacemos tantas partes
iguales (de medida arbitraria)
como las partes en
que queremos dividir
el segmento

1
2
3
A B
3. Unimos la última división
(en este caso la 3ª) con
el otro extremo del segmento
(en este caso el B)

1
2
A B
2´
3
4. Trazamos paralelas al
segmento 3B por los puntos
2 y 1, así obtenemos
sobre el segmento AB los
puntos 1´, 2´, que son
las divisiones a partes
iguales del segmento AB

1
2
3
A B
5. Trazamos paralelas al
segmento 3B por los puntos
2 y 1, así obtenemos
sobre el segmento AB los
puntos 1´, 2´, que son
las divisiones a partes
iguales del segmento AB
1´ 2´

V
TT22.. TTRRAAZZAADDOOSS FFUUNNDDAAMMEENNTTAALLEESS EENN EELL PPLLAANNOO.. PPaarraalleellaass,, PPeerrppeennddiiccuullaarreess,, MMeeddiiaattrriicceess
Operaciones con ÁNGULOS
Construir tres ángulos, iguales al dado a mediante los procedimientos indicados:
a
1. POR PERPENDICULARIDAD ENTRE LADOS
2 MIDIENDO CON EL COMPÁS
3. POR PARALELISMO ENTRE LADOS.

V
a
POR PERPENDICULARIDAD
ENTRE LADOS
Trazamos dos rectas que sean
perpendiculares a cada uno
de los lados del ángulo.
Utiliza la escuadra y el cartabón
para ello

V
V
a
a
POR PERPENDICULARIDAD
ENTRE LADOS
Trazamos dos rectas que sean
perpendiculares a cada uno
de los lados del ángulo.
Utiliza la escuadra y el cartabón
para ello

V
1
2
a
MIDIENDO CON EL COMPÁS
1. Trazamos un arco de medida
arbitraria con centro en el vértice,
que cortará los lados del vértice en
los puntos 1 y 2

V
V´
1
2
2
a
2. Sobre una línea auxiliar situamos
un punto V´ y trazamos un arco de
igual radio al trazado en el ángulo
original

V
V´
1
1´
2
2´
a
3. Medimos con el compás, en
el ángulo dado, la distancia que
hay del punto 1 al 2.
Trazamos un arco con dicha
distancia en el punto 2´, que cortará
al arco trazado con anterioridad
desde V´en el punto 1´

V
V´
1
1´
2
2´
a
4. Uniendo V´con 1´obtenemos
el lado que falta para obtener
un ángulo igual al dado

POR PPARALELISMO
ENTRE LADOS
Trazamos, con ayuda de la
escuadra y el cartabón, paralelas
a los dos lados del ángulo.
Ambas rectas se cortarán en V´
V
V´
a

Construir el ÁNGULO IGUAL A LA SUMA DE LOS DADOS b Y g
b g

b
b
g

b
b
g
g

b
b
g
g
g + b

Construir el ÁNGULO IGUAL A LA DIFERENCIA DE LOS DADOS b Y g
b g

b g
b

b g
g
b

b g
g
b
b-g

a
Construye el ÁNGULO TRIPLE DE a

a
a

a
a aa

a
V
Traza la bisectriz del ángulo a

a
V
A
B
1. Trazamos un arco de
radio arbitrario.
Dicho arco corta los
lados del ángulo en
los puntos A y B

a
V
A C
B
2. Trazamos, desde A y
desde B dos arcos iguales
de radio arbitrario
(la medida ha de ser
mayor de la mitad de la
distancia AB).
Donde se corten ambos
arcos obtendremos
el punto C

a
V
A C
B
3. Unimos V con C y
obtenemos la
BISECTRIZ

Trazar la BISECTRIZ DEL ÁNGULO QUE FORMAN LAS RECTAS r Y s
s
r

r 1.En primer lugar trazamos una
s
línea auxiliar que corte r y s

A
r 2. La recta auxiliar forma cuatro ángulos
s
entre r y s.
Trazamos las bisectrices de
dichos ángulos, que se cortarán
B en dos puntos A y B

s
r
A
B
3. Unimos A y B y obtenemos
la BISECTRIZ

DIVISIÓN DE UN ÁNGULO RECTO EN TRES PARTES IGUALES
V

V
1. Trazamos un arco cualquiera
con centro en V, y obtenemos
los puntos 1 y 2
1
2

V
2. Trazamos el arco 1V, y
obtenemos el punto 3
1
2 3

V
3. Trazamos el arco 2V, y
obtenemos el punto 4
1
2 3
4

V
4. Uniendo V con 3 y 4
trazamos las dos rectas
que dividen el ángulo en
tres partes iguales
1
2 3
4

V
CONSTRUCCIÓN DE ÁNGULOS CON EL COMPÁS
Ángulo de 60º
1
Para hacer un ángulo de 60º nos basamos en la construicción
de un triángulo equilátero. Los ángulos de un triángulo equilátero
miden 60º.
Trazamos un arco arbitrario desde V, obteniendo el punto 1
60º
60º 60º

Ángulo de 60º
V
1
2
Trazamos un arco 1V y obtenemos el punto 2

Ángulo de 60º
V
60º
1
2
Uniendo V2 obtenemos el lado del ángulode 60º que buscamos

Ángulo de 30º
2
V 1
Se comienza realizando un ángulo de 60º
como se ha visto anteriormente

Ángulo de 30º
2
V 1
3
Se realiza la bisectriz del ángulo 2V1,
y ya tenemos el ángulo de 30º

Ángulo de 30º
2
V 1
3
30º

Ángulo de 15º
2
V 1
Comenzamos por hacer un ángulo de 30,
para ello hacemos la bisectriz al de 60 (2V1)

Ángulo de 15º
2
V 1
3

Ángulo de 15º
2
V 1
3
30º

Ángulo de 15º
2
4 3
30º 15º
V 1

Ángulo de 90º
V 1

Ángulo de 90º
2
V 1

Ángulo de 90º
3 2
V 1

T2GG. eeTooRmmAeeZttArrííaaD O33ºS EE FSSUOON D A M E N T A L E S TT ERRNAA ZZEAAL DDPOOLASSN GGOEE. POOaMMraÉÉleTTlRRasIICC, POOeSSrp BBenÁÁdSSicIICCuOOlaSSres, Mediatrices
Ángulo de 90º
4
3 2
V 1

Ángulo de 90º
4
3 2
90º
V 1

Ángulo de 75º
4
3 2
V 1
Se comienza realizando un ángulo de 90º
como se ha visto anteriormente

Ángulo de 45º
4
5
3 2
V 1
Se realiza un ángulo de 90º
90º

Ángulo de 45º
4
5
3 2
V 1
6
45º
Se realiza la bisectriz del ángulo 5V1 de 90º,
90º

TRAZADOS BÁSICOS DE DIBUJO GEOMÉTRICO

Recomendados

Más contenido relacionado

La actualidad más candente (20)

Destacado (20)

Similar a TRAZADOS BÁSICOS DE DIBUJO GEOMÉTRICO (20)

Más de JUAN DIAZ ALMAGRO (19)

Último (20)

TRAZADOS BÁSICOS DE DIBUJO GEOMÉTRICO